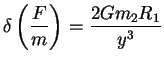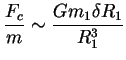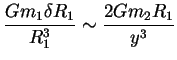suivant: Le moment quadrupôlaire
monter: La hauteur de la
précédent: La hauteur de la
Table des matières
Déterminons simplement l'ordre de grandeur de la hauteur
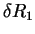 de la déformation (voir la figure 4.3).
de la déformation (voir la figure 4.3).
La masse  produit une accélération différentielle entre la surface
et le centre du corps de masse
produit une accélération différentielle entre la surface
et le centre du corps de masse 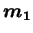 , qui s'exprime selon :
, qui s'exprime selon :
en considérant la gravitation comme seule force 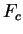 de cohésion ;
celle-ci s'écrit comme la différence entre la gravitation à
l'extérieur du bourrelet
et la gravitation à l'intérieur :
et comme le tout est en équilibre :
ce qui donne :
de cohésion ;
celle-ci s'écrit comme la différence entre la gravitation à
l'extérieur du bourrelet
et la gravitation à l'intérieur :
et comme le tout est en équilibre :
ce qui donne :
 |
(4.1) |
Blanc Guillaume
2000-05-18
![]() de la déformation (voir la figure 4.3).
de la déformation (voir la figure 4.3).
![]() produit une accélération différentielle entre la surface
et le centre du corps de masse
produit une accélération différentielle entre la surface
et le centre du corps de masse ![]() , qui s'exprime selon :
, qui s'exprime selon :