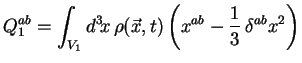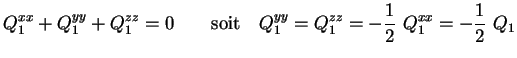suivant: Forme du moment quadrupôlaire
monter: Le moment quadrupôlaire
précédent: Le moment quadrupôlaire
Table des matières
Par définition la composante 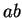 du moment quadrupôlaire du corps (1)
s'écrit :
du moment quadrupôlaire du corps (1)
s'écrit :
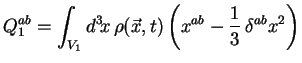 |
(4.2) |
Ainsi, pour l'ellipsoïde allongé (1) on a :
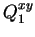 |
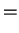 |
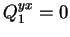 |
(4.3) |
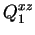 |
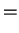 |
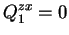 |
(4.4) |
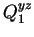 |
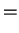 |
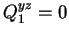 |
(4.5) |
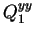 |
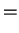 |
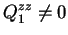 |
(4.6) |
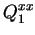 |
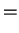 |
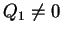 |
(4.7) |
sa trace étant nulle, par définition, soit :
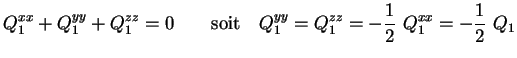 |
(4.8) |
Un tel ellipsoïde de révolution a donc une seule composante du moment
quadrupôlaire indépendante, 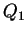 .
.




suivant: Forme du moment quadrupôlaire
monter: Le moment quadrupôlaire
précédent: Le moment quadrupôlaire
Table des matières
Blanc Guillaume
2000-05-18
![]() du moment quadrupôlaire du corps (1)
s'écrit :
du moment quadrupôlaire du corps (1)
s'écrit :