Notations mathématiques

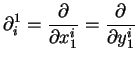
Je note les dérivées partielles spatiales de la façon suivante :

$$\partial^1_i = \frac{\partial}{\partial x_1^i} = \frac{\partial}{\partial y_1^i}$$

suivant le contexte.

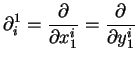
Ou encore :

$$\partial_i = \frac{\partial}{\partial y^i} \qquad \textrm{et} \qquad \partial_{kji} = \frac{\partial^3}{\partial y^k \partial y^j \partial y^i}$$

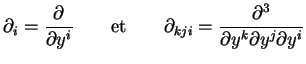
Les dérivés totales par rapport au temps sont notées :

$$\frac{df}{dt} = \dot{f}$$

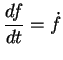
Le produit scalaire entre deux vecteurs $\vec{a}$ et $\vec{b}$ est noté :

$$(ab) = a_ib^i$$ (1)

La somme de deux composantes symétriques d'un tenseur est notée :

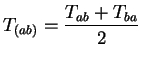$$T_{(ab)} = \frac{T_{ab} + T_{ba}}{2}$$ (2)