



suivant: Définition actuelle
monter: Définition
précédent: Définition
Table des matières
Dans son article Love (1909), s'intéresse aux déformations
de la Terre sous l'effet des forces de marée. Il est ainsi
amené à définir le déplacement radial 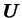 qu'il exprime selon :
qu'il exprime selon :
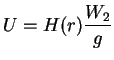 |
(A.1) |
où 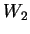 est le potentiel générateur de la marée (par la Lune),
est le potentiel générateur de la marée (par la Lune),
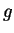 est la valeur
moyenne de la gravité à la surface de la Terre ;
est la valeur
moyenne de la gravité à la surface de la Terre ; 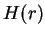 est une fonction
(sans dimension)
du rayon
est une fonction
(sans dimension)
du rayon 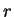 qui dépend du profil de densité.
qui dépend du profil de densité.
De la même façon le potentiel 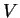 de la Terre déformée par les
forces de marée, s'écrit :
de la Terre déformée par les
forces de marée, s'écrit :
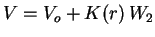 |
(A.2) |
où 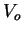 est le potentiel de la Terre non perturbée,
est le potentiel de la Terre non perturbée, 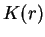 étant
une fonction de
étant
une fonction de 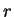 (sans dimension).
Et à la surface de la Terre
(sans dimension).
Et à la surface de la Terre 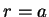 on a :
on a :
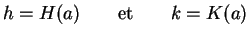 |
(A.3) |




suivant: Définition actuelle
monter: Définition
précédent: Définition
Table des matières
Blanc Guillaume
2000-05-18
![]() qu'il exprime selon :
qu'il exprime selon :
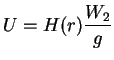
![]() de la Terre déformée par les
forces de marée, s'écrit :
de la Terre déformée par les
forces de marée, s'écrit :