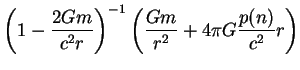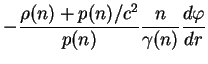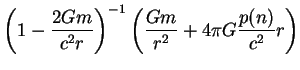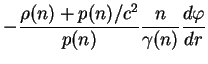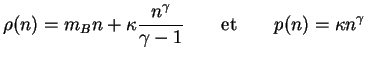suivant: Résultats obtenus
monter: Calcul de pour une
précédent: Calcul de pour une
Table des matières
Pour obtenir le profil de densité d'une étoile à neutron,
j'ai intégré numériquement (par la méthode de Runge-Kutta)
le système différentiel de
Tolman-Oppenheimer-Volkoff qui régit les équilibres hydrostatiques
en relativité générale :
| avec |
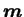 |
la masse contenue dans la sphère de rayon 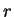 ; ; |
| |
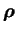 |
la densité d'énergie ; |
| |
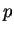 |
la pression ; |
| |
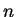 |
la densité baryonique ; |
| |
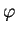 |
le potentiel gravitationnel newtonnien ; |
| |
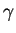 |
est l'indice adiabatique ; |
pour une équation d'état polytropique :
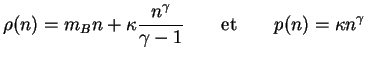 |
(A.18) |
| où |
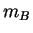 |
est la masse baryonique (
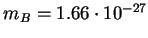 kg) ; kg) ; |
| |
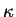 |
est la constante de pression. |
avec
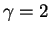 et
et
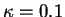 dans le cas où
dans le cas où 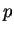 est exprimé en
est exprimé en
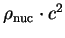 ,
,
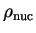 étant la densité
de la matière nucléaire (
étant la densité
de la matière nucléaire (
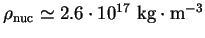 ) ; et
) ; et 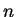 en densité baryonique
nucléaire (
en densité baryonique
nucléaire (
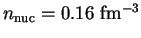 ).
).
Ce modèle est criticable, mais le profil de densité obtenu
est correct au moins sur la forme. De plus il me permet
de déterminer une valeur du nombre de Love, quantité qui n'apparaît
pas dans la littérature sur les équations d'état d'étoiles à
neutron.




suivant: Résultats obtenus
monter: Calcul de pour une
précédent: Calcul de pour une
Table des matières
Blanc Guillaume
2000-05-18