Définition

Dans son étude des systèmes binaires proches, Kopal (1965) définit l'énergie potentielle d'un système binaire proche constitué de deux composantes de masses $m_{1,2}$ et de rayon moyen $a_{1,2}$, dont les centres de gravité sont séparés par le rayon vecteur $r$ de leur orbite relative, qu'il exprime selon :

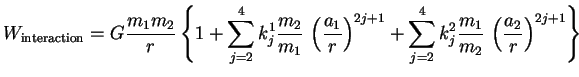$$W_{\textrm{interaction}} = G\frac{m_1m_2}{r} \left\{1 + \sum_{j =... ...m_{j = 2}^{4} k_j^2 \frac{m_1}{m_2}\, \left(\frac{a_2}{r}\right)^{2j+1}\right\}$$ (A.6)

dans le cas où la vitesse de rotation des deux corps est nulle. Les constantes $k^{1,2}_j$ dépendent de la structure interne des étoiles : il les appelle constantes du mouvement apsidien. En fait c'est aussi le nombre de Love tel que défini en (A.5).

Dans l'expression précédente, les sommes représentent la distortion mutuelle due aux forces de marée des deux composantes (correspondant aux 2 $^{\textrm{\\lq eme}}$, 3 $^{\textrm{\\lq eme}}$ et 4 $^{\textrm{\\lq eme}}$ harmoniques pour des distortions superficielles d'une sphére de rayon $a$).

A l'ordre quadrupôlaire (2 $^{\textrm{\\lq eme}}$ harmonique), cela donne :

$$W_{\textrm{interaction}} = G\frac{m_1m_2}{r} \left\{1 + k_2^1 \fr... ...a_1}{r}\right)^5 + k_2^2 \frac{m_1}{m_2}\, \left(\frac{a_2}{r}\right)^5\right\}$$ (A.7)