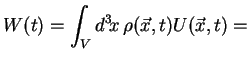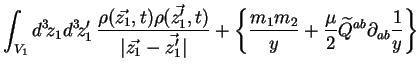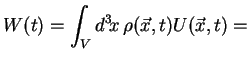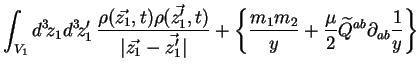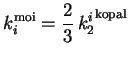Lien entre cette constante et le moment quadrupôlaire

A l'ordre quadrupôlaire, l'énergie potentielle gravitationnelle s'écrit (avec mes notations) :

$$W(t) = { \int_V d^3\!x\, \rho(\vec{x},t) U(\vec{x},t) =}$$

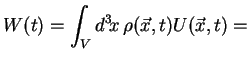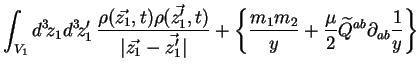$$\int_{V_1} d^3\!z_1 d^3\!z'_1\, \frac{\rho(\vec{z_1},t) \rho(\vec... ...ac{m_1 m_2}{y} + \frac{\mu}{2} \widetilde{Q}^{ab} \partial_{ab} \frac1y\right\}$$ (A.8)

ou encore (d'aprés (4.9)) :

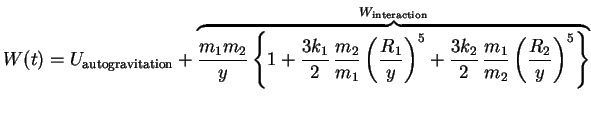$$W(t) = U_{\textrm{autogravitation}} + \overbrace{\frac{m_1 m_2}{y... ...frac{m_1}{m_2} \left(\frac{R_2}{y}\right)^5\right\}}^{W_{\textrm{interaction}}}$$ (A.9)

En comparant (A.7) et (A.9) avec 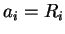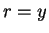$a_i = R_i$, $r = y$, on constate que

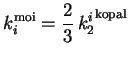$$k_i^{\textrm{moi}} = \frac23\, {k_2^i}^{\textrm{kopal}}$$ (A.10)