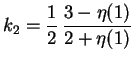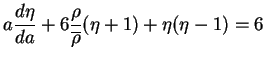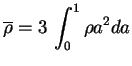suivant: Calcul de pour une
monter: Les constantes du mouvement
précédent: Lien entre cette constante
Table des matières
Le résultat précédent est très intéressant car les constantes de Kopal (1965) s'expriment selon :
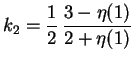 |
(A.11) |
où 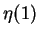 est la valeur à la surface
est la valeur à la surface 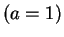 d'une solution
particulière de l'équation différentielle du premier ordre de Radau :
d'une solution
particulière de l'équation différentielle du premier ordre de Radau :
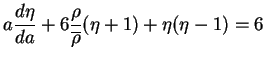 |
(A.12) |
avec la condition initiale :
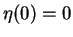 .
.
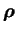 étant la densité à la distance
étant la densité à la distance 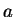 du centre, et
du centre, et
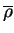 la densité moyenne intérieure à
la densité moyenne intérieure à 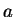 .
.
Par ailleurs, si la densité centrale de l'étoile est élevé,
on montre que la solution exacte de cette équation peut être
approximée par (Kopal (1965), équation (6)) :
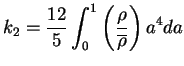 |
(A.13) |
avec :
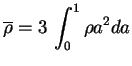 |
(A.14) |




suivant: Calcul de pour une
monter: Les constantes du mouvement
précédent: Lien entre cette constante
Table des matières
Blanc Guillaume
2000-05-18