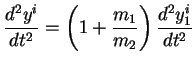suivant: L'énergie du mouvement
monter: L'équation du mouvement
précédent: Equation du mouvement du
Table des matières
Comme le système considéré est isolé (
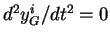 )2.6,
on a la relation :
)2.6,
on a la relation :
avec :
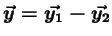 ,
le rayon vecteur du mouvement relatif.
,
le rayon vecteur du mouvement relatif.
D'où l'équation :
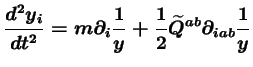 |
(2.11) |
avec :
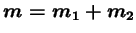 et
et
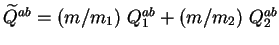 .
.
Blanc Guillaume
2000-05-18
![]() )2.6,
on a la relation :
)2.6,
on a la relation :