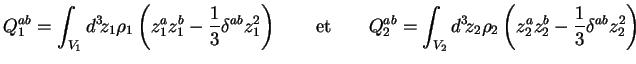suivant: Le mouvement relatif
monter: L'équation du mouvement
précédent: Position du problème
Table des matières
On part de l'expression du vecteur centre d'inertie (2.2), que
l'on dérive deux fois2.3:
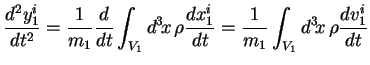 |
(2.7) |
En remplaçant le terme d'accélération par l'expression de l'accélération
d'Euler (2.4), le potentiel gravitationnel 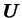 étant
donné par (2.5), on obtient :
étant
donné par (2.5), on obtient :
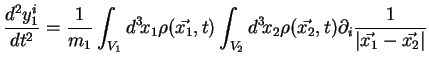 |
(2.8) |
compte tenu du principe de l'action et de la réaction, et du fait
que la pression 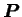 est à support compact.
est à support compact.
En reportant dans cette équation le développement limité
au deuxième ordre2.4
de
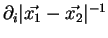 , et avec les
moments quadrupôlaires des deux corps :
, et avec les
moments quadrupôlaires des deux corps :
l'équation du mouvement du corps 1 s'écrit2.5 :
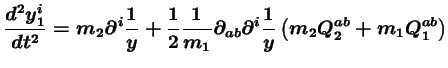 |
(2.10) |




suivant: Le mouvement relatif
monter: L'équation du mouvement
précédent: Position du problème
Table des matières
Blanc Guillaume
2000-05-18
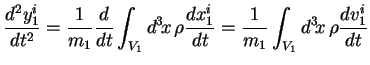
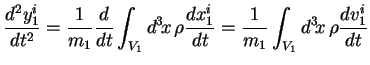
![]() , et avec les
moments quadrupôlaires des deux corps :
, et avec les
moments quadrupôlaires des deux corps :