



suivant: Equation du mouvement du
monter: L'équation du mouvement
précédent: L'équation du mouvement
Table des matières
On considère deux masses fluides en interaction gravitationnelle (voir
figure 2.1).
Les masses 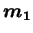 et
et  contenues respectivement dans les volumes
contenues respectivement dans les volumes 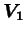 et
et
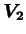 , s'expriment selon :
, s'expriment selon :
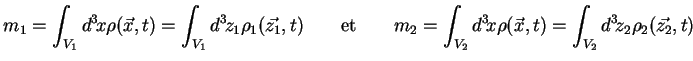 |
(2.1) |
Les vecteurs des centres d'inertie des deux masses, 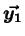 et
et
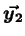 s'écrivent, par définition du barycentre de chacun des deux
corps2.1 :
s'écrivent, par définition du barycentre de chacun des deux
corps2.1 :
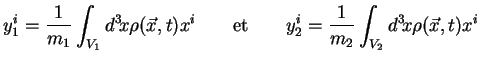 |
(2.2) |
Le système ainsi considéré obéit aux
équations de l'hydrodynamique :
Figure 2.1:
Le système des deux masses fluides, en interaction
gravitationnelle. Ce schéma montre les notations utilisées. L'origine du référentiel (inertiel) dans lequel on se place est le point O.
Les points G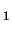 et G
et G sont les centres de masse des corps 1 et 2.
sont les centres de masse des corps 1 et 2.
|
|
Le potentiel gravitationnel pour le système que l'on considère (deux
volumes fluides distincts) s'écrit :
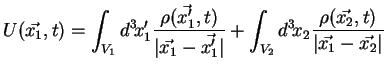 |
(2.5) |




suivant: Equation du mouvement du
monter: L'équation du mouvement
précédent: L'équation du mouvement
Table des matières
Blanc Guillaume
2000-05-18
![]() et
et ![]() contenues respectivement dans les volumes
contenues respectivement dans les volumes ![]() et
et
![]() , s'expriment selon :
, s'expriment selon :
![\includegraphics [angle=270, width=10cm]{systeme.eps}](img96.gif)