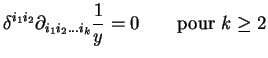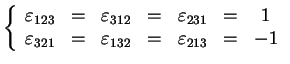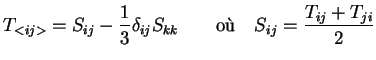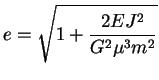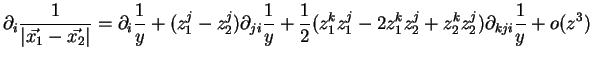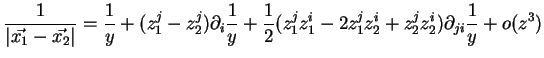- ... l'autre1.1
-
L'étape finale de la coalescence ne sera pas observable par les
interféromètres, puisque les ondes alors émises auront une fréquence
autour du kHz (800
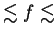 2500 kHz) : le signal sera
perdu dans le bruit de photon. L'observation d'un tel signal permettrait
néanmoins d'obtenir de précieuses informations sur l'équation d'état
de la matière nucléaire.
2500 kHz) : le signal sera
perdu dans le bruit de photon. L'observation d'un tel signal permettrait
néanmoins d'obtenir de précieuses informations sur l'équation d'état
de la matière nucléaire.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... d'Univers1.2
- Car le signal gravitationnel est inversement
proportionnel à la distance (d'aprés (1.2)).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... excentricit\'e1.3
-
Les binaires compactes résultantes de l'évolution stellaire normale
doivent avoir une orbite trés circulaire, car les forces de réaction
au rayonnement gravitationnel circularisent trés rapidement l'orbite ;
mais les systèmes binaires compacts
qui se forment par capture au sein d'un amas d'étoiles dense, peuvent
avoir une orbite
très excentrique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... composantes1.4
-
Un des effets relativistes est le suivant : alors que les ondes émergent
de la binaire, une fraction d'entre elles
rétroagit une ou plusieurs fois sur la courbure de l'espace-temps de la
binaire, produisant des ondes de ``queue''. Ces queues agissent en retour
sur la binaire, modifiant son taux de décroissance orbitale d'une
manière mesurable.
Par ailleurs, si le moment cinétique orbital est incliné
par rapport au spin des composantes, chacun des moments cinétiques va
précesser autour du moment cinétique total. Et cette précession va
induire une modulation sur les ondes, d'où un deuxième effet relativiste
(interaction spin-spin et spin-orbite).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... r\'eduit1.5
-
Il est donc plus important d'avoir les contributions Post-Newtoniennes
sur la phase
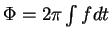 de façon très précise, par rapport
aux modulations Post-Newtoniennes sur l'amplitude (Cutler et al.
(1993)).
de façon très précise, par rapport
aux modulations Post-Newtoniennes sur l'amplitude (Cutler et al.
(1993)).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Irrotationnels1.6
-
Les ellipsoïdes de Roche-Riemann sont des généralisations des ellipsoïdes
de Roche, qui incluent, en plus de la fréquence orbitale, des rapports variables
de la vorticité sur le moment cinétique de rotation. La viscosité étant finie,
l'étoile ne sera jamais exactement sur la séquence de Roche, à cause de la dissipation
qui entraîne une évolution continuelle de l'orbite.
Dans les ellipsoïdes de Roche, le fluide est stationnaire dans le repère tournant
(il tourne à vitesse orbitale dans le repère inertiel).
Dans les solutions de Roche-Riemann (les plus générales), seule la forme de l'étoile
est en corotation avec le mouvement orbital.
Par contre, pour les ellipsoïdes de Roche-Riemann Irrotationnels
(avec une vorticité nulle), le fluide a seulement
un mouvement oscillant
dans le repère inertiel (il tourne exactement dans le sens contraire du mouvement orbital,
dans le repère tournant).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
corps2.1
- A travers l'ensemble de ce rapport, les indices (en lettres
latines) prennent les trois valeurs des coordonnées spatiales.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)2.2
- Dans la plupart des calculs qui ponctuent
ces pages, on prend les constantes :
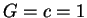 ,
sauf si elles sont indiquées clairement dans la formule !
,
sauf si elles sont indiquées clairement dans la formule !
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fois2.3
-
Pour toute fonction
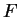 de
de 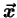 et de
et de 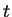 , caractéristique d'un élément de fluide de
volume
, caractéristique d'un élément de fluide de
volume 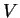 et de densité
et de densité 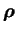 , on a :
, on a :
 |
(2.6) |
relation qui se demontre aisément en utilisant l'équation de continuité,
et compte tenu que les grandeurs comme la densité 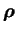 ou la pression
ou la pression 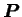 sont à support compact.
sont à support compact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ordre2.4
-
Le développement limité au second ordre de
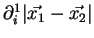 est donné par :
est donné par :
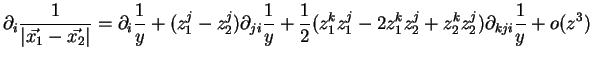 |
(2.9) |
en notant
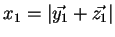 ,
,
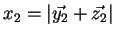 et
et
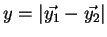 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... s'\'ecrit2.5
- Sachant que l'on a :
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)2.6
-
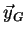 étant le rayon vecteur du centre de masse
étant le rayon vecteur du centre de masse 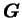 des deux corps
(
des deux corps
(
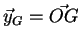 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... obtient2.7
-
Le développement limité au second ordre de
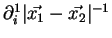 s'écrit :
s'écrit :
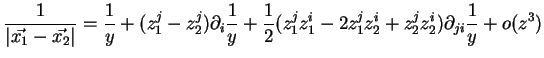 |
(2.31) |
avec
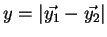 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
antisym\'etrique2.8
-
La composante
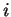 du produit vectoriel des deux vecteurs
du produit vectoriel des deux vecteurs 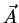 et
et
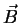 s'ecrit :
s'ecrit :
 |
(2.36) |
où
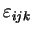 est le pseudo-tenseur complètement antisymétrique :
est le pseudo-tenseur complètement antisymétrique :
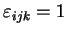 |
si 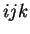 est une permutation paire de est une permutation paire de 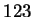 ; ; |
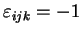 |
si 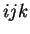 est une permutation impaire de est une permutation impaire de 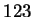 ; ; |
 |
si deux indices sont identiques. |
Ainsi :
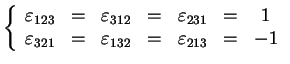 |
(2.37) |
On a aussi :
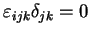 |
(2.38) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trace3.1
-
Les tenseurs sans trace : notation compacte.
On note le tenseur ``sans trace'' 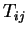 comme
comme 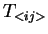 , avec :
On montre qu'avec cette notation :
, avec :
On montre qu'avec cette notation :
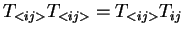 |
(3.11) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... a3.2
- Attention ! Ces expressions
ne sont valables que derrière un tenseur symétrique en
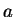 et
et 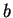 et sans trace !
et sans trace !
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ponctuelles3.3
- L'émission d'ondes gravitationnelles finit par
circulariser les orbites : le cas présent est donc tout à fait réaliste.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... circulariser4.1
- En effet,
l'excentricité d'un mouvement keplerien s'exprime selon :
où
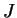 est le moment cinétique du système (
est le moment cinétique du système (
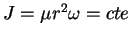 pour
un tel système), et
pour
un tel système), et 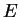 son énergie ; les effets de marée dissipant
de l'énergie de façon irréversible,
son énergie ; les effets de marée dissipant
de l'énergie de façon irréversible, 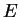 diminue, donc
diminue, donc 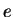 tend vers
0 (orbite ciculaire).
tend vers
0 (orbite ciculaire).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)4.2
- Ces valeurs sont typiques pour des étoiles à neutron.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.