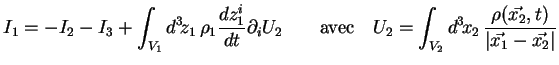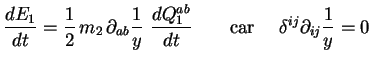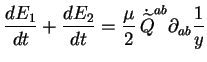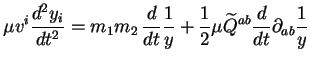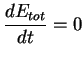suivant: Le moment cinétique
monter: Application à notre système
précédent: L'énergie totale
Table des matières
Nous allons vérifier que l'énergie totale 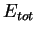 est bien constante
en exprimant les variations temporelles des énergies internes
est bien constante
en exprimant les variations temporelles des énergies internes 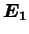 et
et
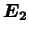 des
deux corps en fonction des moments quadrupôlaires associés.
des
deux corps en fonction des moments quadrupôlaires associés.
D'après la relation (2.27), on a :
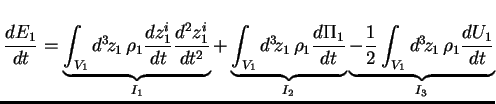 |
|
|
(2.29) |
où :
 |
(2.30) |
Je développe l'intégrale 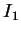 , avec
, avec
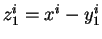 , puis en insérant l'accélération d'Euler
(2.4), et avec les résultats du §2.2.1,
j'obtiens :
, puis en insérant l'accélération d'Euler
(2.4), et avec les résultats du §2.2.1,
j'obtiens :
En incorporant le développement limité de
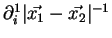 , on obtient2.7 à l'ordre quadrupôlaire :
Le calcul s'effectue pareillement pour
, on obtient2.7 à l'ordre quadrupôlaire :
Le calcul s'effectue pareillement pour 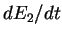 .
Les variations temporelles des énergies internes des corps ``1'' et ``2''
s'écrivent donc :
.
Les variations temporelles des énergies internes des corps ``1'' et ``2''
s'écrivent donc :
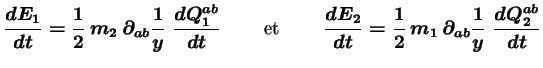 |
(2.32) |
donc, comme il se doit,
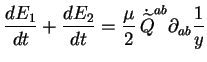 |
(2.33) |
avec l'équation du mouvement (2.11) multipliée scalairement par 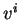 :
:
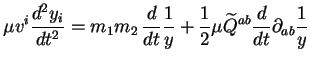 |
(2.34) |
cela donne (à partir de (2.26)) :
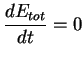 |
(2.35) |
L'énergie totale est donc bien conservée.




suivant: Le moment cinétique
monter: Application à notre système
précédent: L'énergie totale
Table des matières
Blanc Guillaume
2000-05-18
![]() est bien constante
en exprimant les variations temporelles des énergies internes
est bien constante
en exprimant les variations temporelles des énergies internes ![]() et
et
![]() des
deux corps en fonction des moments quadrupôlaires associés.
des
deux corps en fonction des moments quadrupôlaires associés.
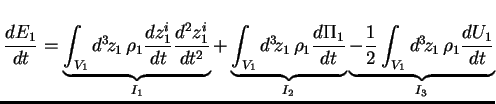

![]() , avec
, avec
![]() , puis en insérant l'accélération d'Euler
(2.4), et avec les résultats du §2.2.1,
j'obtiens :
, puis en insérant l'accélération d'Euler
(2.4), et avec les résultats du §2.2.1,
j'obtiens :