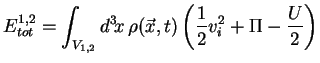Application à notre système

Utilisons le résultat (2.20) obtenu au §2.2.1 pour le système qui nous intéresse ici : deux masses fluides en interaction gravitationnelle. L'énergie totale d'un tel système est égale à la somme de l'énergie totale du corps 1 et du corps 2 :

$$E_{tot} = E^1_{tot} + E^2_{tot}$$

avec :

$$E^{1,2}_{tot} = \int_{V_{1,2}} d^3\!x\, \rho(\vec{x},t) \left(\frac{1}{2} v_i^2 + \Pi - \frac{U}{2}\right)$$

Nous allons maintenant expliciter chacun des trois termes de cette intégrale.