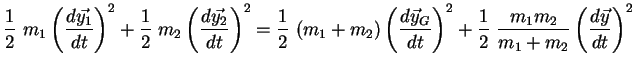Les termes d'énergie cinétique et d'énergie interne

Le premier terme de l'expression (2.20), intégré sur le volume 1, devient, sachant que $x^i = y_1^i + z_1^i$ :

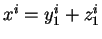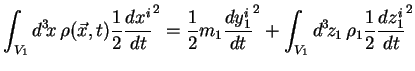$$\int_{V_{1}} d^3\!x\, \rho(\vec{x},t) \frac{1}{2} \frac{dx^i}{dt}... ... \frac{dy_1^i}{dt}^2 + \int_{V_1} d^3\!z_1\, \rho_1 \frac12 \frac{dz_1^i}{dt}^2$$ (2.21)

On fait la même chose sur le volume 2.

A partir des relations :

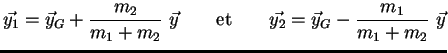$$\vec{y_1} = \vec{y}_G + \frac{m_2}{m_1+m_2}\ \vec{y} \qquad \textrm{et} \qquad \vec{y_2} = \vec{y}_G - \frac{m_1}{m_1+m_2}\ \vec{y}$$ (2.22)

On peut transformer la somme des énergies cinétiques orbitales des deux corps en une énergie cinétique ``relative'' :

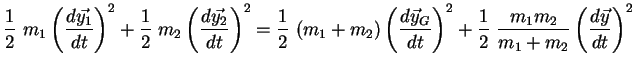$$\frac12\ m_1 \left(\frac{d\vec{y_1}}{dt}\right)^2 + \frac12\ m_2 ... ...}\right)^2 + \frac12\ \frac{m_1m_2}{m_1+m_2} \left(\frac{d\vec{y}}{dt}\right)^2$$ (2.23)

Le deuxième terme de (2.20), l'énergie interne thermodynamique, dépend de l'équation d'état du fluide ; celle-ci étant inconnue dans le cas général, on le laisse tel quel.