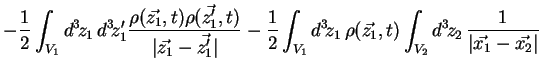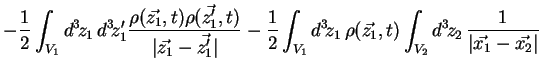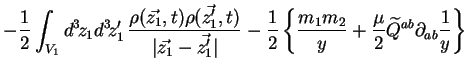suivant: L'énergie totale
monter: Application à notre système
précédent: Les termes d'énergie cinétique
Table des matières
Le troisième terme dans l'expression de l'énergie s'écrit :
 |
| |
|
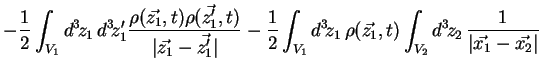 |
(2.24) |
En reportant dans le deuxième terme de droite le développement limité
de
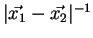 donné par (2.31),
on obtient :
donné par (2.31),
on obtient :
 |
| |
|
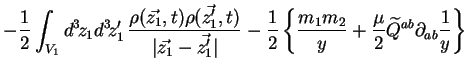 |
(2.25) |
où 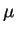 est la masse réduite du système (
est la masse réduite du système (
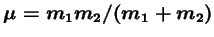 ).
).
On fait le même travail sur le volume 2 (les calculs sont identiques,
il suffit de remplacer les indices ``1'' par des indices ``2'').
Blanc Guillaume
2000-05-18