On multiplie vectoriellement l'équation d'Euler par ![]() ,
en intégrant
sur le volume
,
en intégrant
sur le volume ![]() du fluide :
du fluide :
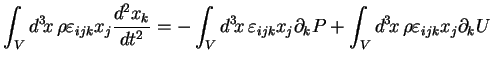
Soit :
Par la suite, on exprime le potentiel gravitationnel ![]() , compte tenu
du fait que le volume
, compte tenu
du fait que le volume ![]() est scindé en deux volumes
est scindé en deux volumes ![]() et
et ![]() pour le cas qui nous concerne.
On développe à l'ordre quadrupôlaire, compte tenu de
(2.9).
Ce qui donne :
pour le cas qui nous concerne.
On développe à l'ordre quadrupôlaire, compte tenu de
(2.9).
Ce qui donne :
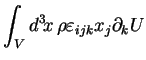 |
![$\displaystyle \underbrace{
m_1m_2 \varepsilon_{ijk} y_j \partial_k \frac1y}_{=\...
... z_1^l +
m_1 \int_{V_2} d^3\!z_2\, \rho_2 z_2^j z_2^l\right]}_{\scriptstyle{1}}$](img195.gif) |
||
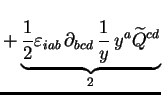 |
(2.40) |
![$\displaystyle \varepsilon_{ijk} \frac{-\delta^{kl}y^2 + 3y^ky^l}{y^5} \left[
m_...
...!z_1\, \rho_1 z_1^j z_1^l +
m_1 \int_{V_2} d^3\!z_2\, \rho_2 z_2^j z_2^l\right]$](img199.gif) |
|||
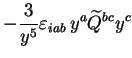 |
(2.41) |
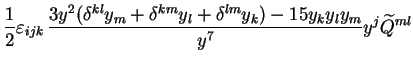 |
|||
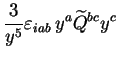 |
(2.42) |
Donc :
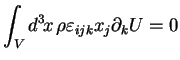 |
(2.43) |
Ainsi (2.39) s'écrit :
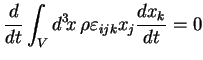 |
(2.44) |
Le moment cinétique total ![]() de deux fluides en interaction
gravitationnelle mutuelle est donc constant, tel que :
de deux fluides en interaction
gravitationnelle mutuelle est donc constant, tel que :