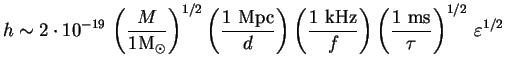 |
(1.2) |
| où | est la masse de la source ; | |
| est sa distance ; | ||
| est la fréquence de l'onde ; | ||
| est le temps que dure l'émission ; | ||
|
|
|
|
| (énergie émise sous forme d'ondes gravitationnelles sur énergie de masse). |
Pour un système binaire compact (
![]() ),
),
![]() ,
,
![]() kHz et
kHz et
![]() ms. Ainsi, pour un tel objet
situé à l'extérieur de la Galaxie (
ms. Ainsi, pour un tel objet
situé à l'extérieur de la Galaxie (
![]() Mpc),
l'amplitude de l'onde est seulement
Mpc),
l'amplitude de l'onde est seulement
![]() !!
!!
Pour une supernova,
![]() , l'amplitude
est ainsi beaucoup plus petite :
, l'amplitude
est ainsi beaucoup plus petite :
![]()