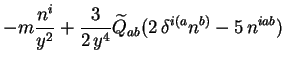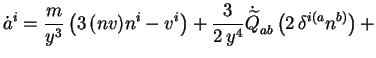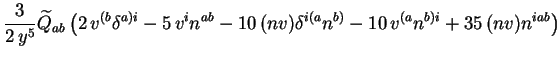suivant: La luminosité gravitationnelle
monter: Le calcul de
précédent: La dérivée troisième par
Table des matières
Elévation au carré
On a :
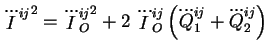 |
(3.16) |
On élève (3.15) au carré, ce qui donne, compte tenu de
(3.11) :
![$\displaystyle {\dddot{I}_O^{ij}}^2 = 4 \mu^2 \left[9\ v^{<i}a^{j>}\ v^{i}a^{j} + y^2\ n^{<i}\dot{a}^{j>}\ n^i\dot{a}^j + 6y\ v^{<i}a^{j>}\ y^i\dot{a}^j \right]$](img267.gif) |
(3.17) |
On calcule ces différents termes en y portant les expressions de 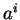 et
et
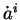 , dans lesquelles on explicite les dérivées partielles
successives de
, dans lesquelles on explicite les dérivées partielles
successives de 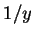 .
.
Avec :
Et compte tenu du fait que le tenseur du moment quadrupôlaire est
symétrique et sans trace, on a3.2 :
où les parenthèses sur les indices représentent une symétrie (
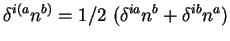 ).
On a donc :
).
On a donc :
où j'ai utilisé la notation
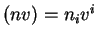 pour les produits scalaires.
pour les produits scalaires.
Tout calcul fait, j'obtiens le résultat suivant :
Par ailleurs, on a
car
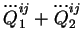 est sans trace et symétrique.
est sans trace et symétrique.
Donc, en définitive, compte tenu de 3.24 et 3.25, j'obtiens :
où 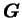 est la constante de la gravitation.
est la constante de la gravitation.




suivant: La luminosité gravitationnelle
monter: Le calcul de
précédent: La dérivée troisième par
Table des matières
Blanc Guillaume
2000-05-18
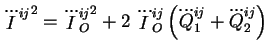
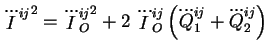
![$\displaystyle {\dddot{I}_O^{ij}}^2 = 4 \mu^2 \left[9\ v^{<i}a^{j>}\ v^{i}a^{j} + y^2\ n^{<i}\dot{a}^{j>}\ n^i\dot{a}^j + 6y\ v^{<i}a^{j>}\ y^i\dot{a}^j \right]$](img267.gif)
![]() et
et
![]() , dans lesquelles on explicite les dérivées partielles
successives de
, dans lesquelles on explicite les dérivées partielles
successives de ![]() .
.