



suivant: Cas non perturbé
monter: Cas d'une orbite circulaire
précédent: La loi de Kepler
Table des matières
Approche perturbative du mouvement circulaire
Je considère une orbite qui serait circulaire (de rayon 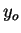 constant et de
pulsation orbitale
constant et de
pulsation orbitale 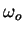 consatnte) pour des masses
ponctuelles3.3,
perturbée par la présence des deux corps de taille finie.
Ainsi :
consatnte) pour des masses
ponctuelles3.3,
perturbée par la présence des deux corps de taille finie.
Ainsi :
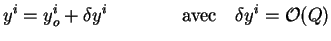 |
(3.40) |
Pour ce faire, on se place en coordonnées cylindriques
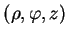 , dans
la base orthonormée
, dans
la base orthonormée
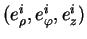 .
.
Sous-sections
Blanc Guillaume
2000-05-18
![]() constant et de
pulsation orbitale
constant et de
pulsation orbitale ![]() consatnte) pour des masses
ponctuelles3.3,
perturbée par la présence des deux corps de taille finie.
Ainsi :
consatnte) pour des masses
ponctuelles3.3,
perturbée par la présence des deux corps de taille finie.
Ainsi :