



suivant: Le mouvement perturbé
monter: Approche perturbative du mouvement
précédent: Approche perturbative du mouvement
Table des matières
Dans ce cas, on obtient, sur cette base :
De plus, on a :
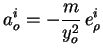 |
(3.44) |
En égalisant les composantes sur 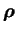 de (3.43) et (3.44),
on retrouve la
de (3.43) et (3.44),
on retrouve la
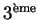 loi de Kepler :
loi de Kepler :
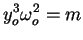 |
(3.45) |
Blanc Guillaume
2000-05-18