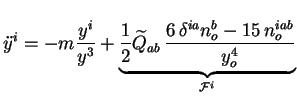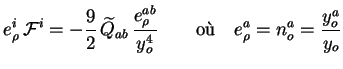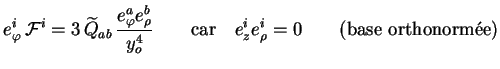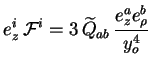suivant: Les effets de marée
monter: Approche perturbative du mouvement
précédent: Cas non perturbé
Table des matières
La perturbation
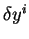 s'écrit :
s'écrit :
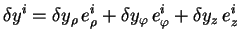 |
(3.46) |
Et donc, on a :
Par ailleurs :
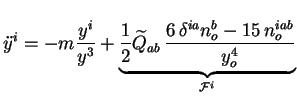 |
(3.50) |
La force ``massique''
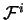 se décompose sur la base
cylindrique de la façon
suivante :
se décompose sur la base
cylindrique de la façon
suivante :
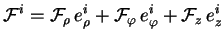 |
(3.51) |
avec :
On obtient ainsi le
système
différentiel vérifié par les composantes de la perturbation, suivant
(avec
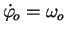 ) :
) :
Dans le chapitre suivant, nous allons considérer une configuration
particulière des composantes de la binaire ; ce qui nous permettra
d'exprimer les moments quadrupôlaires en fonctions des variables
du problème, et de trouver une solution particulière au système
ci-dessus (orbite circulaire).




suivant: Les effets de marée
monter: Approche perturbative du mouvement
précédent: Cas non perturbé
Table des matières
Blanc Guillaume
2000-05-18
![]() s'écrit :
s'écrit :