La $3^{\textrm {\\lq eme}}$ loi de Kepler

La loi de Kepler habituelle $r^3\omega^2 = G(m_1+m_2)$ est vraie pour deux masses ponctuelles en orbite circulaire (sinon il faut remplacer le rayon $r$ par le demi-grand axe de l'ellipse). Je vais donc déterminer la loi équivalente pour deux quadrupôles en orbite l'un autour de l'autre.

Pour cela, projetons l'équation du mouvement (2.11) sur $y_i$ :

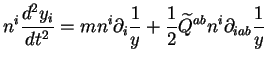$$n^i \frac{d^2y_i}{dt^2} = m n^i\partial_i \frac1y + \frac12 \widetilde{Q}^{ab} n^i\partial_{iab} \frac1y$$ (3.35)

or :

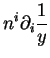$$n^i\partial_i \frac1y = -\frac{1}{y^2}$$ (3.36)

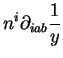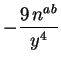$$n^i\partial_{iab} \frac1y = -\frac{9\, n^{ab}}{y^4}$$ (3.37)

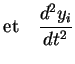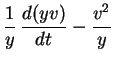$$\textrm{et} \quad \frac{d^2y_i}{dt^2} = \frac1y\, \frac{d(yv)}{dt} - \frac{v^2} {y}$$ (3.38)

Ce qui donne :

$$yv^2 = m + \frac{9}{2\, y^2} \widetilde{Q}_{ab} n^{ab} + y\, \dot{(yv)}$$ (3.39)