



suivant: La loi de Kepler
monter: Expression des perturbations
précédent: Expression des perturbations
Table des matières
Le moment quadrupôlaire a été évalué au §4.2 dans un
référentiel lié au corps considéré.
Or, auparavant nous avons considéré le mouvement dans un référentiel
inertiel ; mais dans le cas étudié ici, les quadrupôles sont fixes
dans le référentiel tournant.
On passe des composantes du moment quadrupôlaire dans le référentiel inertiel
aux composantes dans le référentiel en rotation par :
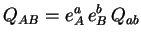 |
(4.10) |
où 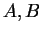 désigne le repère tournant, tandis que
désigne le repère tournant, tandis que 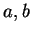 désigne
le repère fixe.
Ainsi, en revenant au système de coordonnées cylindriques du §3.3.2,
les composantes du moment quadrupôlaire sur les axes liés au mouvement orbital,
sont :
désigne
le repère fixe.
Ainsi, en revenant au système de coordonnées cylindriques du §3.3.2,
les composantes du moment quadrupôlaire sur les axes liés au mouvement orbital,
sont :
Ainsi le système différentiel pour les composantes de la perturbation
(équations (3.55),
(3.56) et (3.57)) devient :
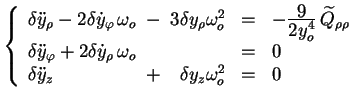 |
(4.14) |
La solution générale de ce système est, en supposant que la projection
sur l'axe ( ) du moment
quadrupôlaire est constante sur une période :
) du moment
quadrupôlaire est constante sur une période :
où 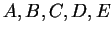 et
et 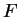 sont des constantes.
sont des constantes.
Ainsi, il existe une solution circulaire (
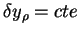 ), dans le
plan
), dans le
plan 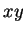 (
(
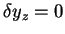 ), si on choisi :
), si on choisi :
De plus
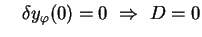 .
Ce qui donne finalement :
.
Ce qui donne finalement :
On obtient bien ainsi un mouvement circulaire.




suivant: La loi de Kepler
monter: Expression des perturbations
précédent: Expression des perturbations
Table des matières
Blanc Guillaume
2000-05-18
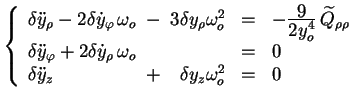
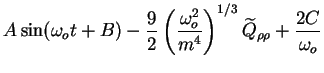
![$\displaystyle 2 A \cos (\omega_o t + B) + \left[9 \left(\frac{\omega_o^5}{m^4}\right)^{1/3}
\widetilde{Q}_{\rho \rho} - 3C\right]\ t + D$](img418.gif)
![]() ), dans le
plan
), dans le
plan ![]() (
(
![]() ), si on choisi :
), si on choisi :