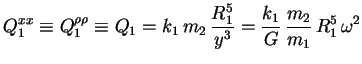suivant: L'énergie totale
monter: La phase orbitale
précédent: La phase orbitale
Table des matières
Compte tenu de la relation (4.9) et de la loi de Kepler
(4.25), on a :
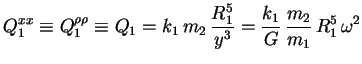 |
(4.27) |
ou encore, pour le corps 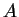 (
(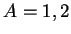 ) :
) :
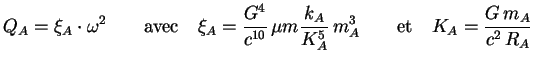 |
(4.28) |
où 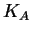 est la compacité du corps (A).
est la compacité du corps (A).
De même :
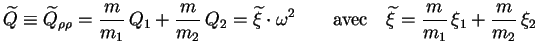 |
(4.29) |
Blanc Guillaume
2000-05-18