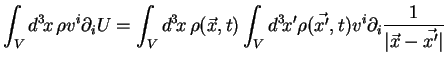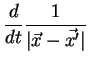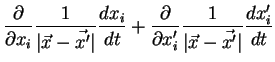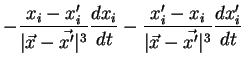L'énergie potentielle

Le potentiel gravitationnel 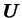$U$ est égal, d'une manière générale, à :

$$U(\vec{x},t) = \int_V d^3\!x' \frac{\rho (x',t)}{\vert \vec{x}-\vec{x'} \vert}$$ (2.16)

Donc le terme 3 de l'équation (2.12) devient :

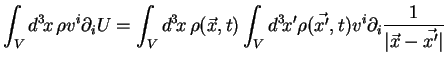$$\int_V d^3\!x\, \rho v^i \partial_i U = \int_V d^3\!x\, \rho(\vec... ...V d^3\!x' \rho(\vec{x'},t) v^i \partial_i \frac{1}{\vert\vec{x}-\vec{x'} \vert}$$ (2.17)

On cherche à transformer les dérivées partielles sur les variables d'espace, en dérivées totales par rapport au temps. Compte tenu du fait que :

$$\frac{d}{dt} \frac{1}{\vert\vec{x}-\vec{x'}\vert} = \frac{\partial}{\partial x_i} \frac{1}{\vert\vec{x}-\vec{x'}\vert... ...\partial} {\partial x'_i} \frac{1}{\vert\vec{x}-\vec{x'}\vert} \frac{dx'_i}{dt}$$

$$= -\frac{x_i-x'_i} {\vert\vec{x}-\vec{x'}\vert^3} \frac{dx_i}{dt} - \frac{x'_i-x_i}{\vert\vec{x}-\vec{x'}\vert^3} \frac{dx'_i}{dt}$$ (2.18)

on en déduit :

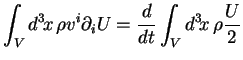$$\int_V d^3\!x\, \rho v^i \partial_i U = \frac{d}{dt} \int_V d^3\!x\, \rho \frac{U}{2}$$ (2.19)