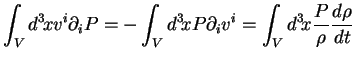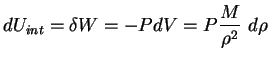suivant: L'énergie potentielle
monter: A partir de l'équation
précédent: L'énergie cinétique
Table des matières
L'énergie interne
En intégrant le terme 2 de (2.12) par parties, on obtient :
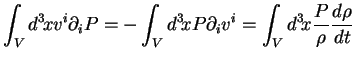 |
(2.14) |
d'après l'équation de continuité.
De plus, le Premier Principe de la Thermodynamique, pour un
système isolé, nous donne :
où 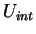 est l'énergie interne du système, W le travail,
est l'énergie interne du système, W le travail,
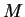 la masse du système,
la masse du système, 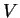 son volume et
son volume et 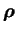 sa densité.
Si on note
sa densité.
Si on note
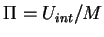 l'énergie interne massique, on obtient
l'énergie interne massique, on obtient
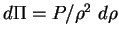 donc
donc
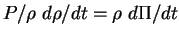 .
En reportant dans l'intégrale (2.14),
cela donne :
.
En reportant dans l'intégrale (2.14),
cela donne :
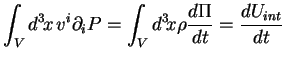 |
(2.15) |
Blanc Guillaume
2000-05-18