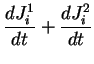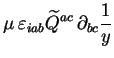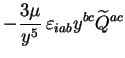suivant: Le moment cinétique est
monter: Application
précédent: Application
Table des matières
On peut développer l'expression générale du moment cinétique
(2.45) pour notre système binaire, sachant que
pour le volume 1,
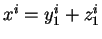 , et pour le volume 2,
, et pour le volume 2,
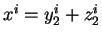 ; cela donne :
; cela donne :
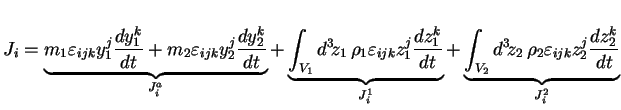 |
(2.46) |
Compte tenu de (2.22), le premier terme
ci-dessus s'écrit :
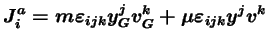 |
(2.47) |
Tandis que 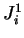 et
et 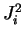 s'écrivent sous la forme :
s'écrivent sous la forme :
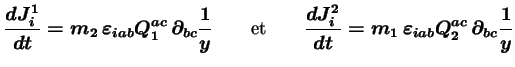 |
(2.48) |
donc :
Blanc Guillaume
2000-05-18
![]() , et pour le volume 2,
, et pour le volume 2,
![]() ; cela donne :
; cela donne :