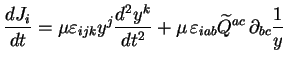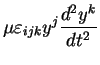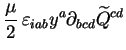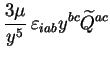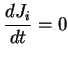Le moment cinétique est conservé

Calculons (d'après (2.46)) :

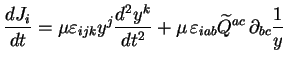$$\frac{dJ_i}{dt} = \mu \varepsilon_{ijk} y^j \frac{d^2y^k}{dt^2} + \mu\, \varepsilon_{iab} \widetilde{Q}^{ac}\, \partial_{bc} \frac1y$$ (2.50)

avec, compte tenu de (2.11) :

$$\mu \varepsilon_{ijk} y^j \frac{d^2y^k}{dt^2} = \frac{\mu}{2}\, \varepsilon_{iab} y^a \partial_{bcd} \widetilde{Q}^{cd}$$

$$= \frac{3\mu}{y^5}\, \varepsilon_{iab} y^{bc} \widetilde{Q}^{ac}$$ (2.51)

On a donc bien :

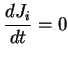$$\frac{dJ_i}{dt} = 0$$ (2.52)

Le moment cinétique est donc conservé au cours du mouvement.