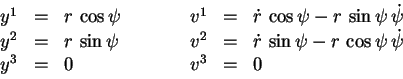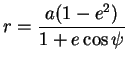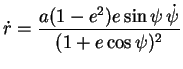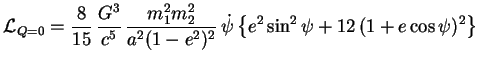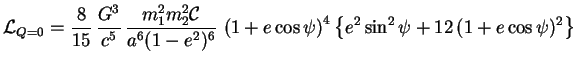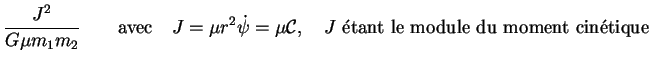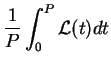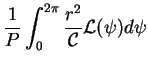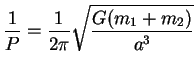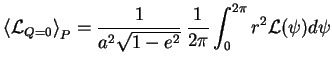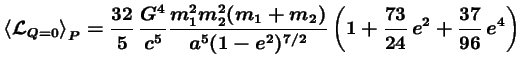suivant: Cas d'une orbite circulaire
monter: La luminosité gravitationnelle
précédent: La luminosité gravitationnelle
Table des matières
On peut se placer dans le cas abondamment étudié des masses ponctuelles.
Pour ce faire, il suffit d'annuler les moments quadrupôlaires dans l'expression
(3.27) ci-dessus. Cela donne :
![$\displaystyle \mathcal{L}_{Q=0} = \mu^2 \frac{G^3}{5\,c^5}\,\left[32\, \frac{m^2v^2}{y^4} -\frac{88}{3}\, \frac{m^2(nv)^2}{y^4}\right]$](img300.gif) |
(3.28) |
Je peux développer cette expression en exprimant ses différents termes
en coordonnées polaires  dans le plan de l'orbite :
dans le plan de l'orbite :
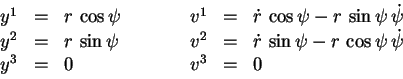 |
(3.29) |
ce qui fait que :
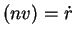 et
et
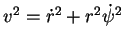 .
.
En outre, le mouvement est purement képlérien, la trajectoire est donc
elliptique, et son équation est donnée par :
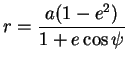 |
(3.30) |
où 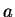 est le demi-grand axe de l'ellipse et
est le demi-grand axe de l'ellipse et 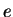 son excentricité.
Avec :
son excentricité.
Avec :
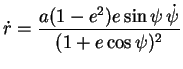 |
(3.31) |
on a tous les éléments pour exprimer (3.28) en fonction des
coordonnées polaires 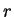 et
et  , et des paramètres
, et des paramètres 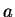 et
et 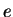 de
l'ellipse. Ce qui donne :
De plus, on a
de
l'ellipse. Ce qui donne :
De plus, on a
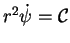 , où
, où
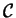 est une
constante du mouvement (constante des Aires).
Donc :
Par ailleurs, le paramètre
est une
constante du mouvement (constante des Aires).
Donc :
Par ailleurs, le paramètre 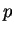 de l'ellipse est tel que :
de l'ellipse est tel que :
Cela permet d'en déduire
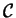 :
soit :
:
soit :
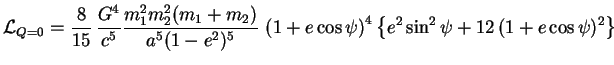 |
(3.32) |
Le taux moyen d'émission d'ondes gravitationnelles est obtenu en moyennant
(3.32) sur une période orbitale 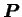 :
:
La période orbitale étant donnée par la troisième loi de Kepler :
soit :
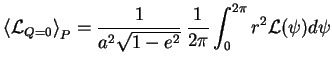 |
(3.33) |
où
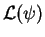 est donné par (3.32).
Ce qui donne finalement :
est donné par (3.32).
Ce qui donne finalement :
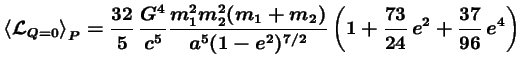 |
(3.34) |
J'ai ainsi retrouvé le résultat obtenu par Peters et Mathews (1963).




suivant: Cas d'une orbite circulaire
monter: La luminosité gravitationnelle
précédent: La luminosité gravitationnelle
Table des matières
Blanc Guillaume
2000-05-18
![$\displaystyle \mathcal{L}_{Q=0} = \mu^2 \frac{G^3}{5\,c^5}\,\left[32\, \frac{m^2v^2}{y^4} -\frac{88}{3}\, \frac{m^2(nv)^2}{y^4}\right]$](img300.gif)
![]() dans le plan de l'orbite :
dans le plan de l'orbite :