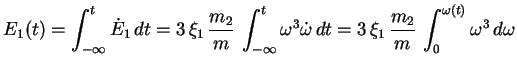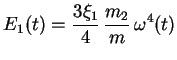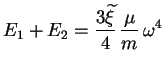suivant: Variation de l'énergie avec
monter: L'énergie totale
précédent: L'énergie totale
Table des matières
L'énergie interne du corps (1) est telle que :
or :
soit :
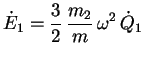 |
(4.31) |
avec
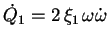 d'après (4.28).
d'après (4.28).
Pour obtenir l'expression de l'énergie interne, on intègre entre 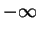 et
et 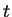 , ce qui donne :
, ce qui donne :
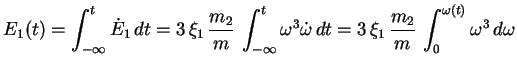 |
(4.32) |
car
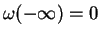 .
.
Donc :
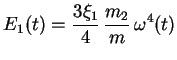 |
(4.33) |
ainsi :
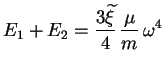 |
(4.34) |
et l'énergie totale (4.30) peut s'écrire :
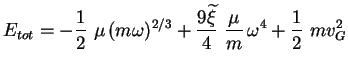 |
(4.35) |




suivant: Variation de l'énergie avec
monter: L'énergie totale
précédent: L'énergie totale
Table des matières
Blanc Guillaume
2000-05-18
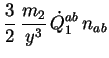
![$\displaystyle \frac32\, \frac{m_2}{y^3}\,
\left[\frac{d\left(Q_1^{ab}\,n_{ab}\right)}{dt} - Q_1^{ab}\,
\frac{d(n_{ab})}{dt}\right]$](img451.gif)
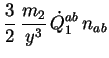
![$\displaystyle \frac32\, \frac{m_2}{y^3}\,
\left[\frac{d\left(Q_1^{ab}\,n_{ab}\right)}{dt} - Q_1^{ab}\,
\frac{d(n_{ab})}{dt}\right]$](img451.gif)
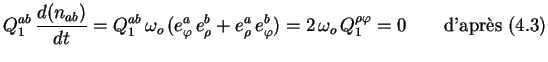
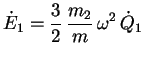
![]() et
et ![]() , ce qui donne :
, ce qui donne :